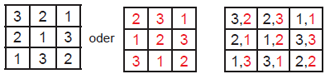
The problem of the 36 officers

The Russian Empress Catherine commissioned the Swiss mathematician Leonhard Euler (1707-1783) in 1766 to solve a dance problem. 36 officers with six different ranks from six different regiments were to be arranged on a square area in such a way that in each row and each column, an officer of a regiment and a rank stands. In mathematics, this is the problem of finding two orthogonal Latin squares of order 6.

For example, a Latin square of order 3 consists of 3 rows and 3 columns, with the numbers 1 to 3 appearing only once in each row and each column:

Two different Latin squares are called orthogonal if, when superimposed, each ordered pair appears only once (see above).

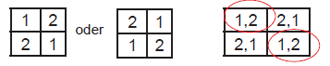
There are a total of twelve Latin squares of order 3, but only two of order 2. These are not orthogonal because when superimposed, their combinations appear more than once:

At order 6, which Euler dealt with, there are indeed 576 different Latin squares; however, it is impossible to combine any two of them to be orthogonal. Interestingly, except for orders 2 and 6, orthogonal Latin squares can be found for all other orders.

Euler himself suspected that Catherine's task could not be solved, a conjecture that was only proven by the French mathematician Gaston Terry in 1902. The squares are called Latin because Euler used Latin letters instead of numbers. Orthogonal Latin squares are also called Greek-Latin squares, as Greek letters were used for the second square. Over the centuries, this problem has led to important work in combinatorics. Latin squares also play a role in error correction procedures.

Image caption: Orthogonal Latin square of order 10: colored sand on Kappa lightweight board (50 x 50 cm).